Multi-Dimensional Signal Alignment
Local All-Pass Filter Framework
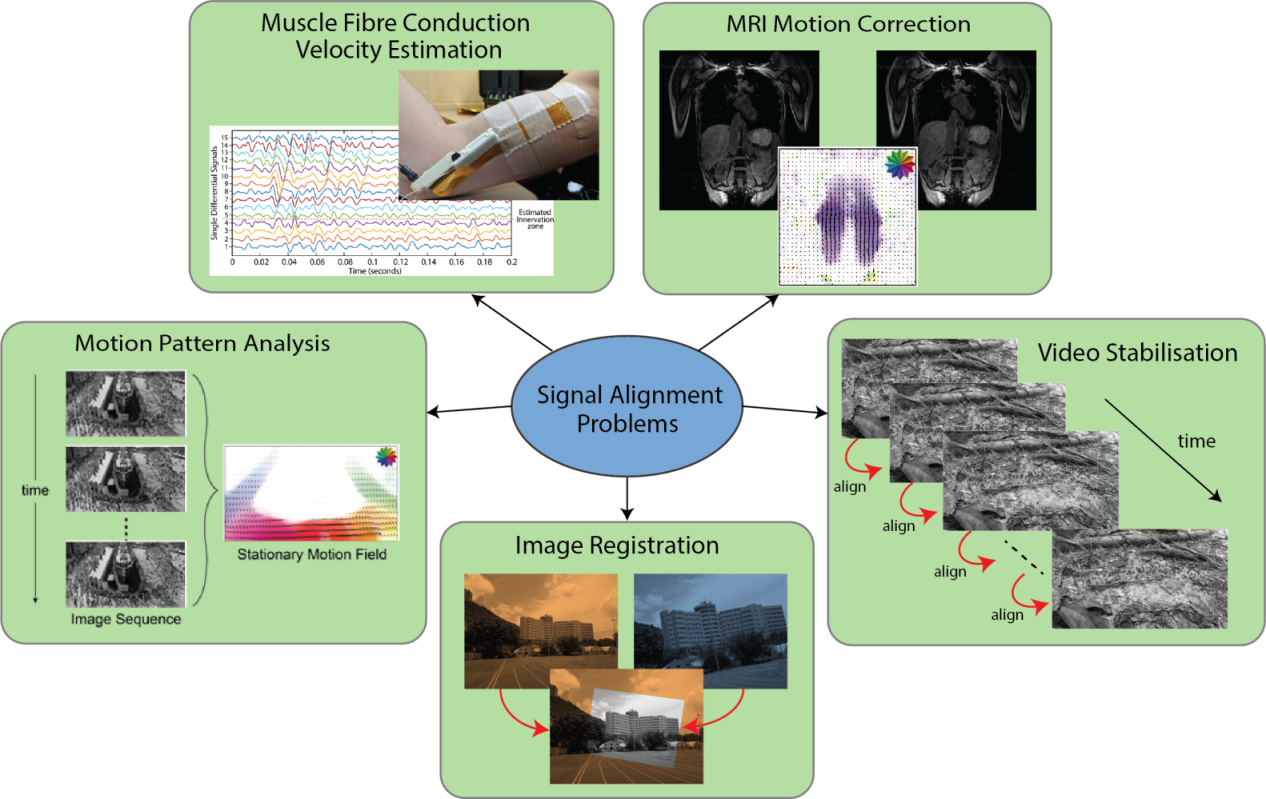
The estimation of a geometric transformation that aligns two or more signals is a problem that has many applications in signal processing. The problem occurs when signals are either recorded from two or more spatially separated sensors or when a single sensor is recording a time-varying scene. Examples of fundamental tasks that involve this problem are shown in the figure below. In this project we estimate the transformation between these signals using a novel local all-pass (LAP) filtering framework.
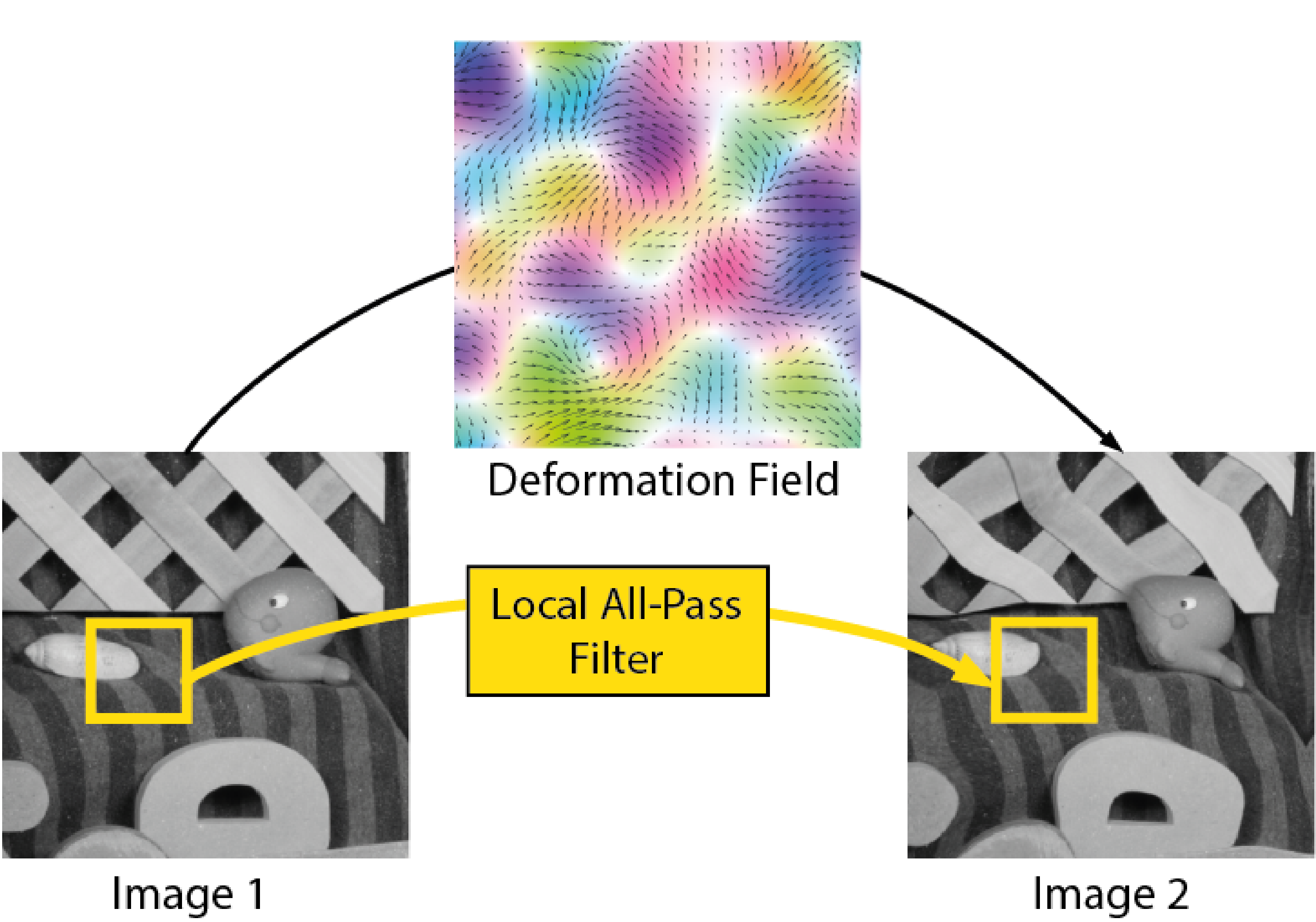
The underlying principle in our LAP framework is that, on a local level, the geometric transformation between a pair of signals can be approximated as a rigid deformation which is equivalent to an all-pass filtering operation. Thus, efficient estimation of the all-pass filter in question allows an accurate estimation of the local geometric transformation between the signals. Accordingly, repeating this estimation for every sample/pixel/voxel in the signals results in a dense estimation of the whole geometric transformation. This processing chain can be performed efficiently and achieve very accurate results. We have applied this framework to image registration [1], [2], [3], motion correction [4], [5] and time-varying delay estimation [6].
Remark: This problem is both restrictive, as the brightness consistency is unlikely to be satisfied exactly, and ill-posed as, for \(n>1\) many deformations many satisfy the equation and most are meaningless. However, in many applications, it is important to determine a meaningful deformation field.To overcome these challenges, we assume the deformation field is slowly varying such that locally it is equivalent to a rigid deformation and apply our local all-pass filter framework.

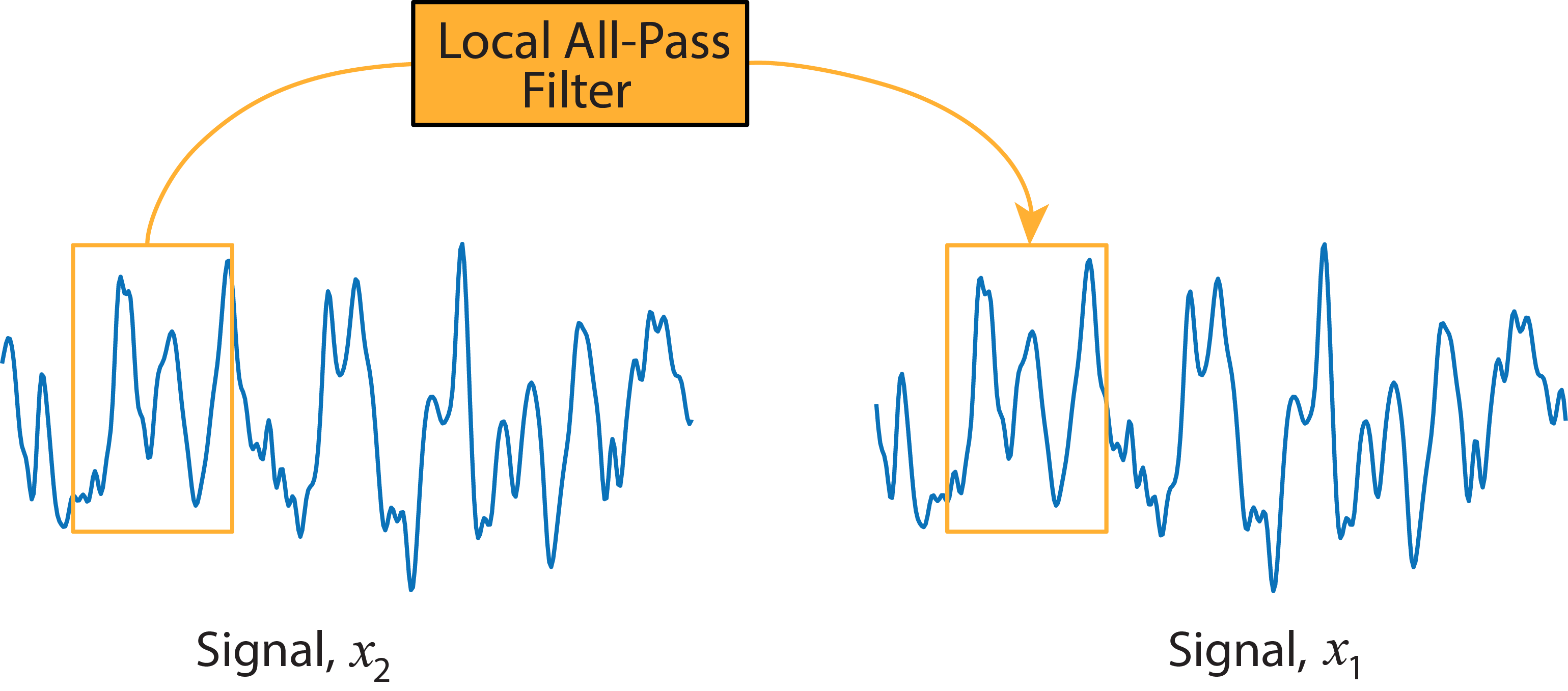
To allow for a non-rigid deformation, we limit this estimation to a small local region, estimate a local all-pass filter and extract a local estimate of the deformation. This local estimate corresponds to the centre of the region. Accordingly, a dense, per-sample, deformation estimate is obtained by repeating this process for all the samples in the signal using a sliding-window mechanism, see figure below. Importantly, as discussed in [1] this can be performed very efficiently.

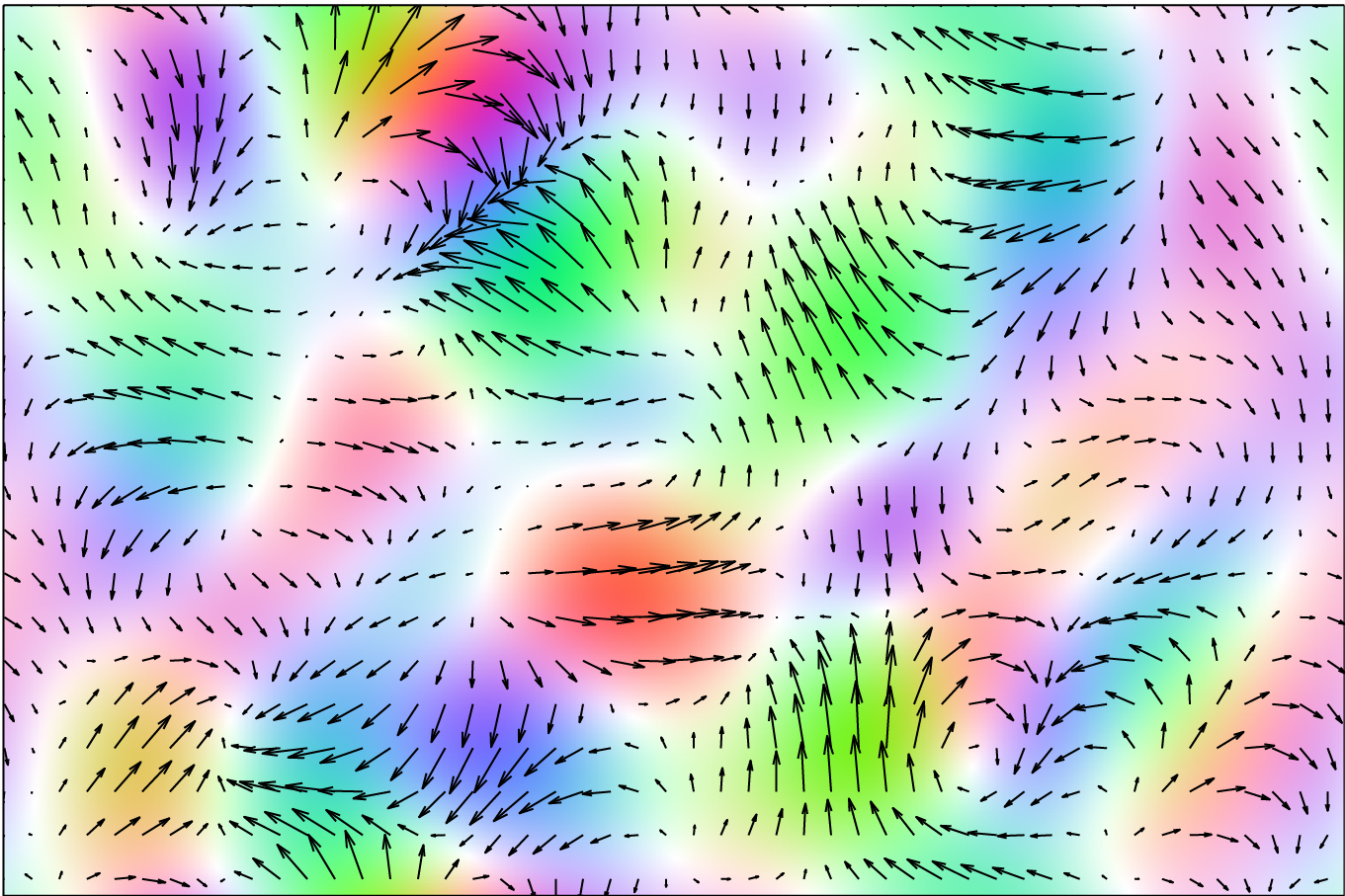

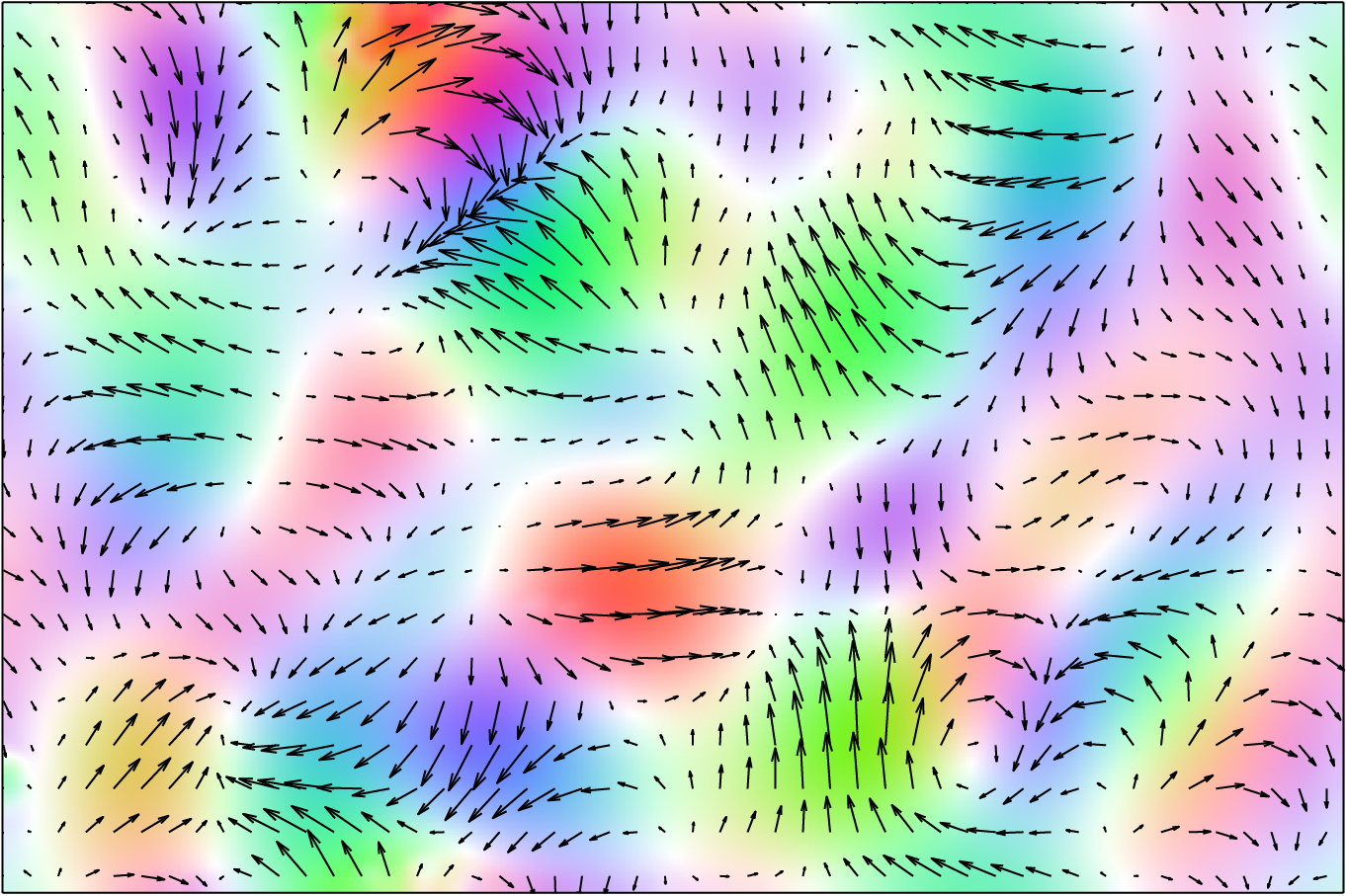

To allow estimation of both slowly and quickly varying deformations, we use an iterative poly-filter LAP framework that starts with large filters estimating the deformation, aligning the images and then repeating with a smaller filter [1].
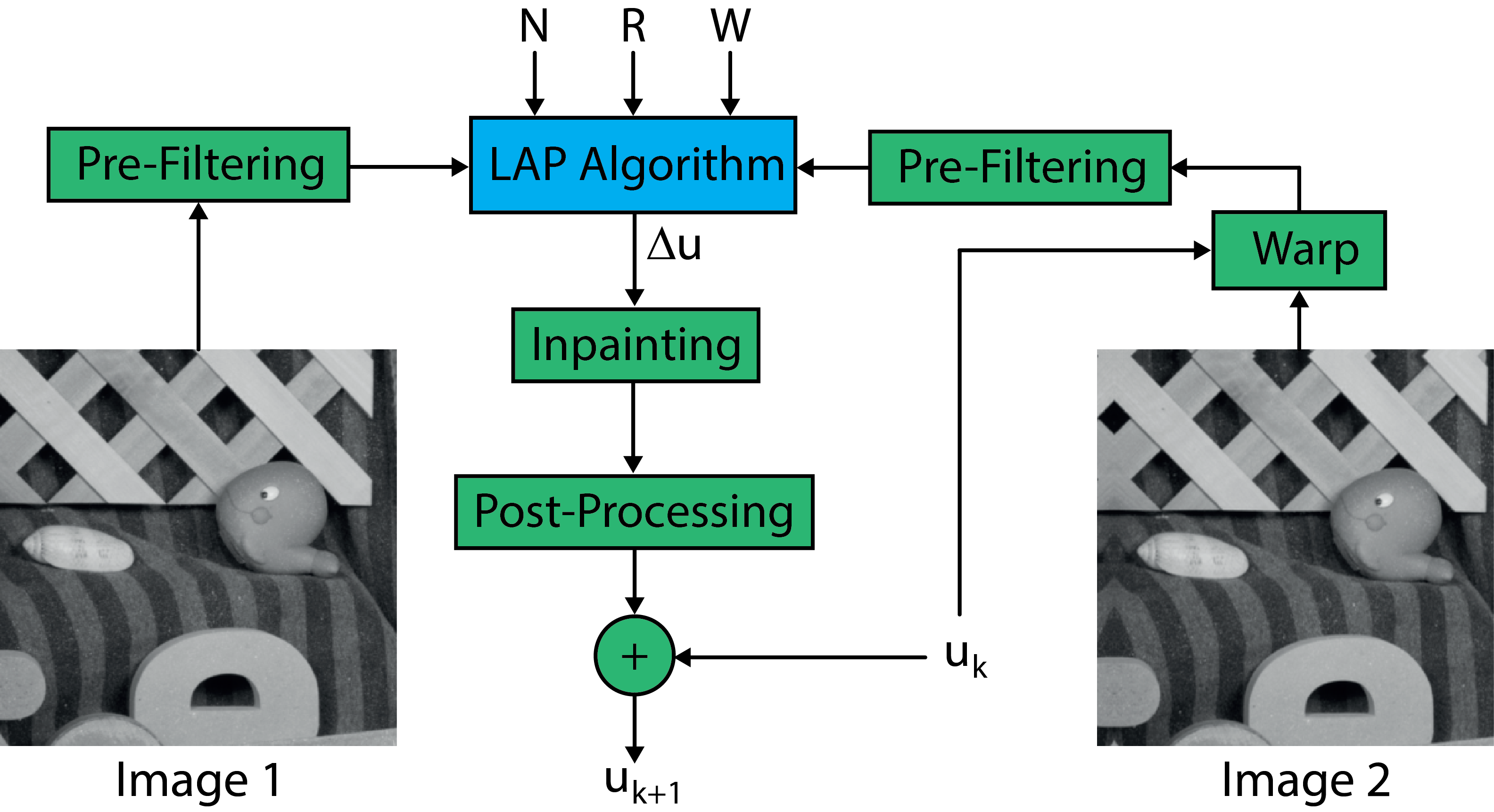
Parametric Registration
For parametric image registration, we introduce a quadratic parametric model for the deformation and iteratively estimate the parameters of the model [3], [8], [9]. This parametric extension is robust to model mis-match (noise, blurring, etc), very accurate and capable of handling very large deformations. Furthermore, by modeling intensity variations, the parametric LAP is capable of handling multi-modal registration problems.


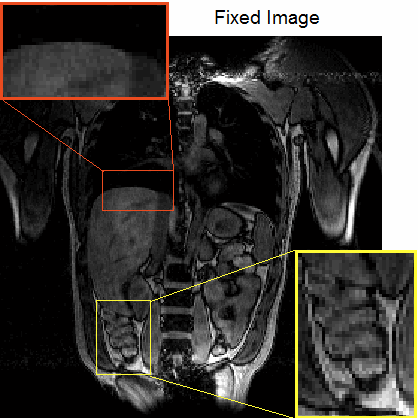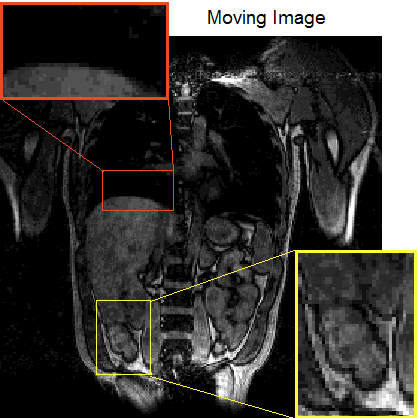
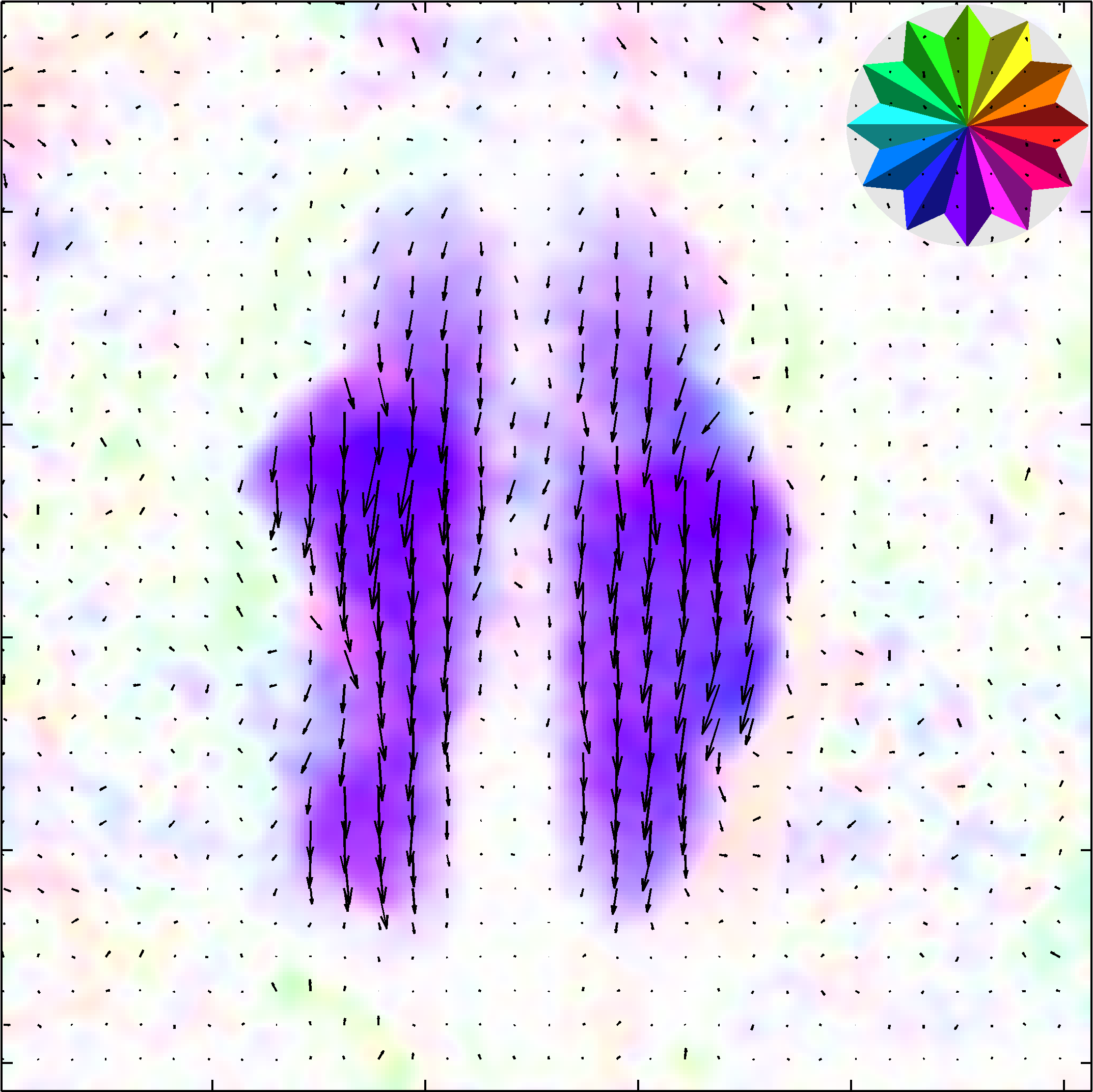

To allow estimation of both slowly and quickly varying deformations, we use an iterative poly-filter 3D LAP framework that starts with large filters estimating the deformation, aligning the images and then repeating with a smaller filter [10].
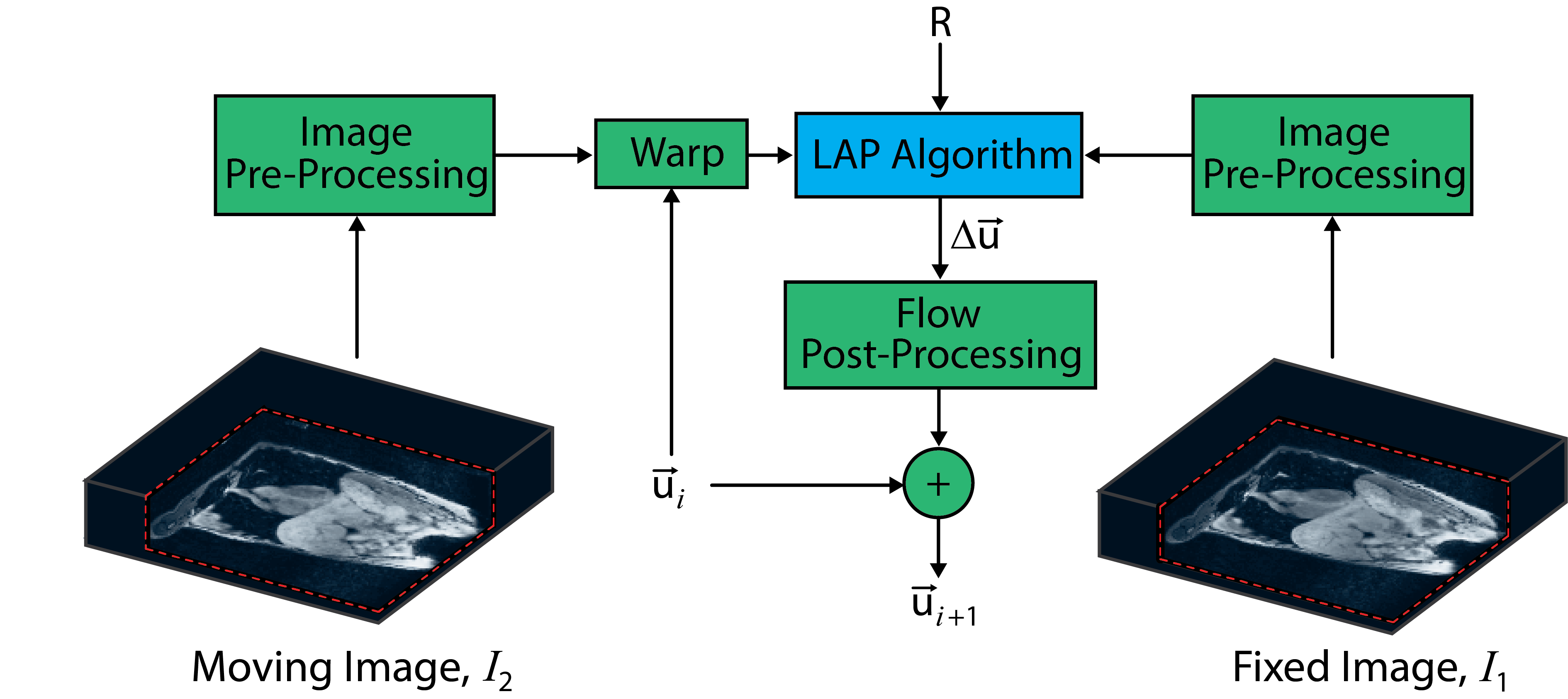
LAP + Deep Learning
More recently, the LAP framework has been combined with a deep learning architecture to allow robust motion correction when faced with highly-accelerated, undersampled, MRI data [11]. This network has also been combined with a reconstruction network to allow motion-corrected reconstruction of 4D (3D + time) MRI data [12], [13]. The architecture of this LAP deep learning network (LAPNet) is shown below.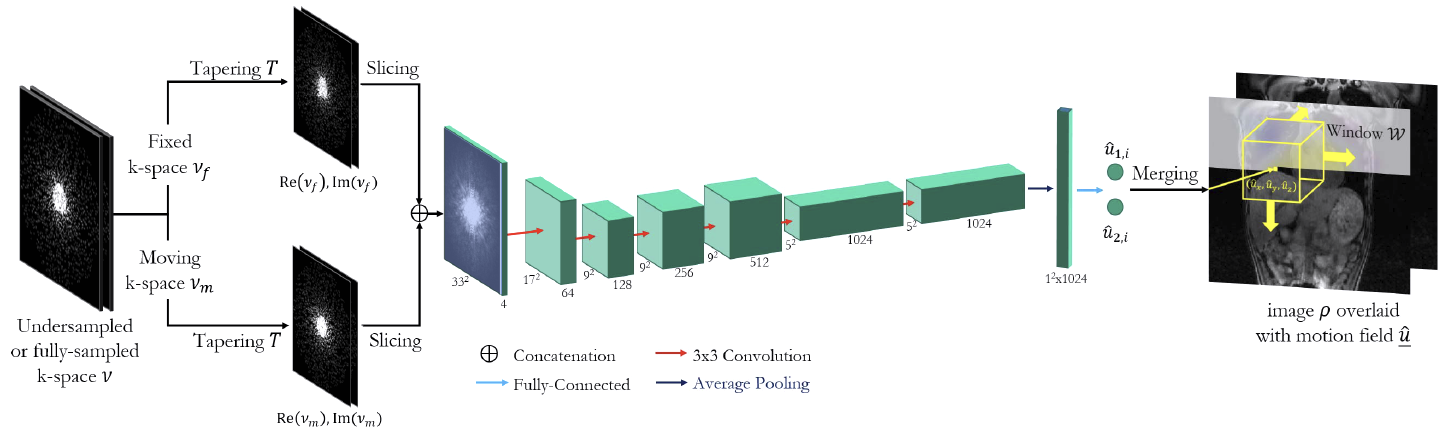
High-Density Surface EMG (HD-sEMG):
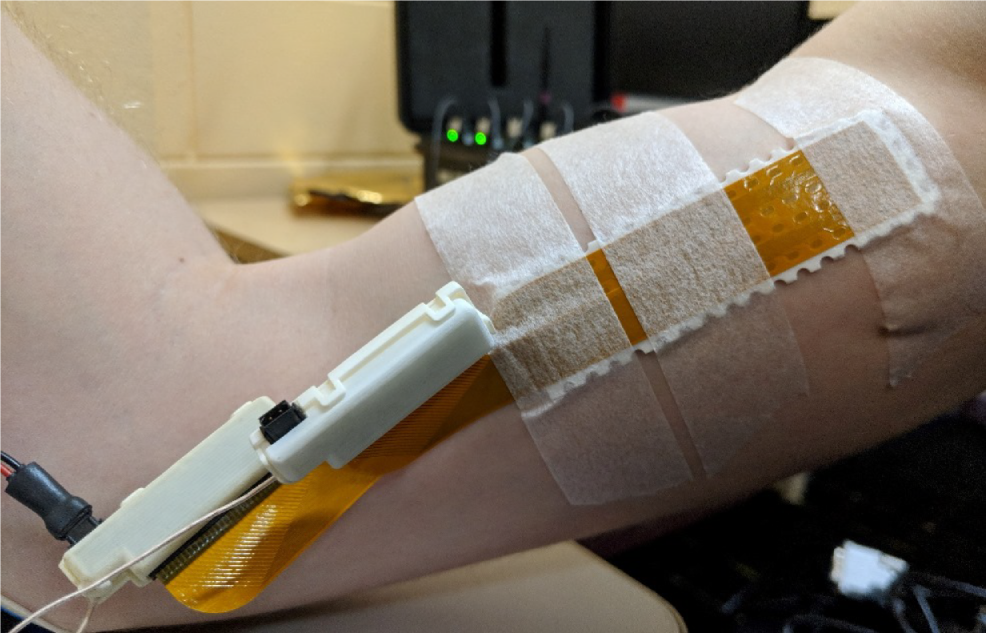
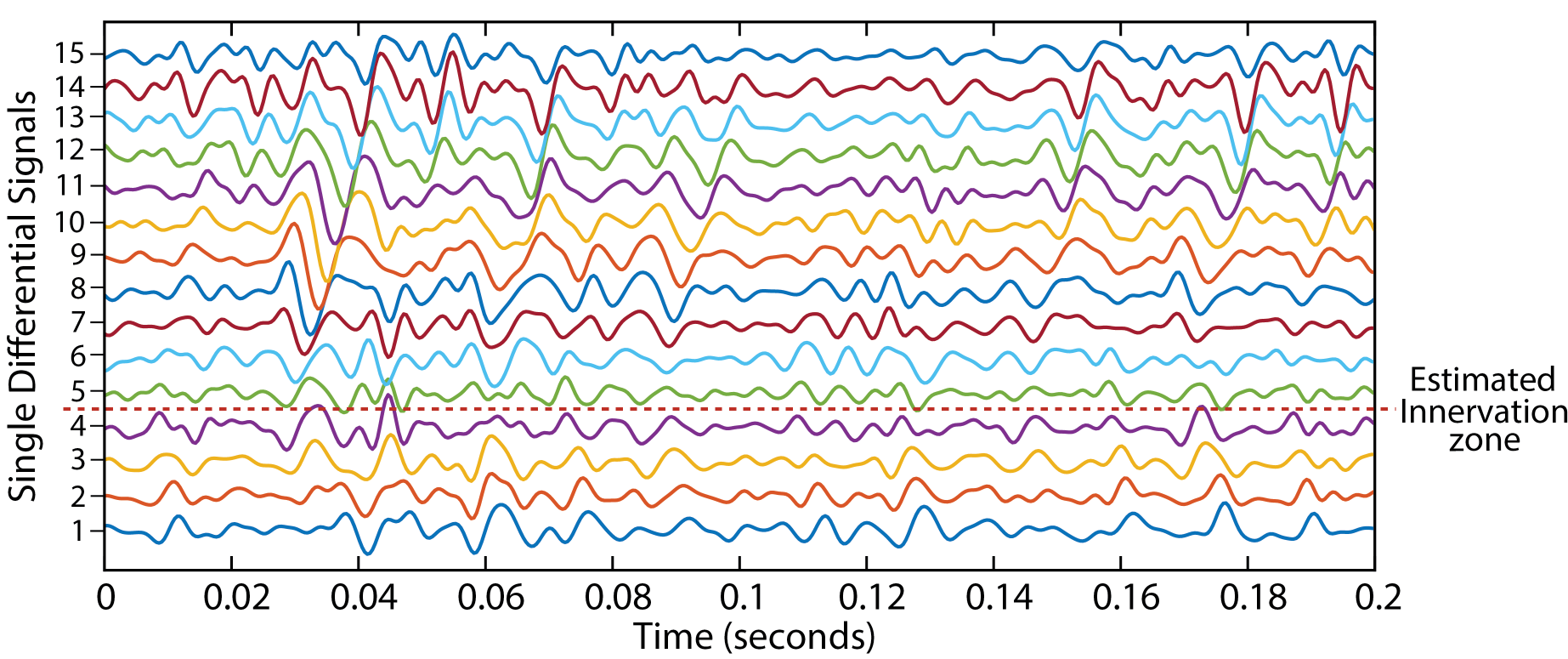
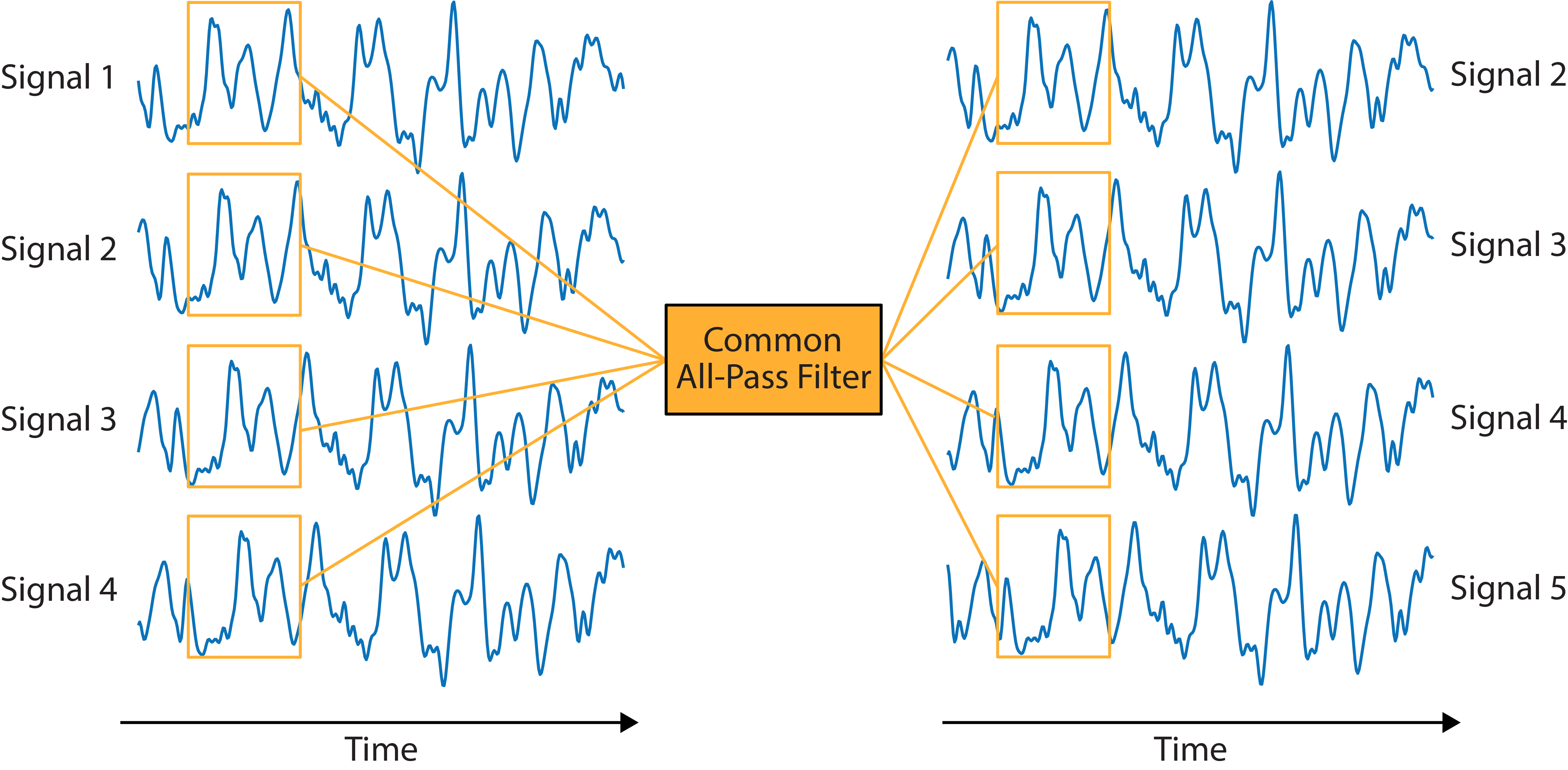
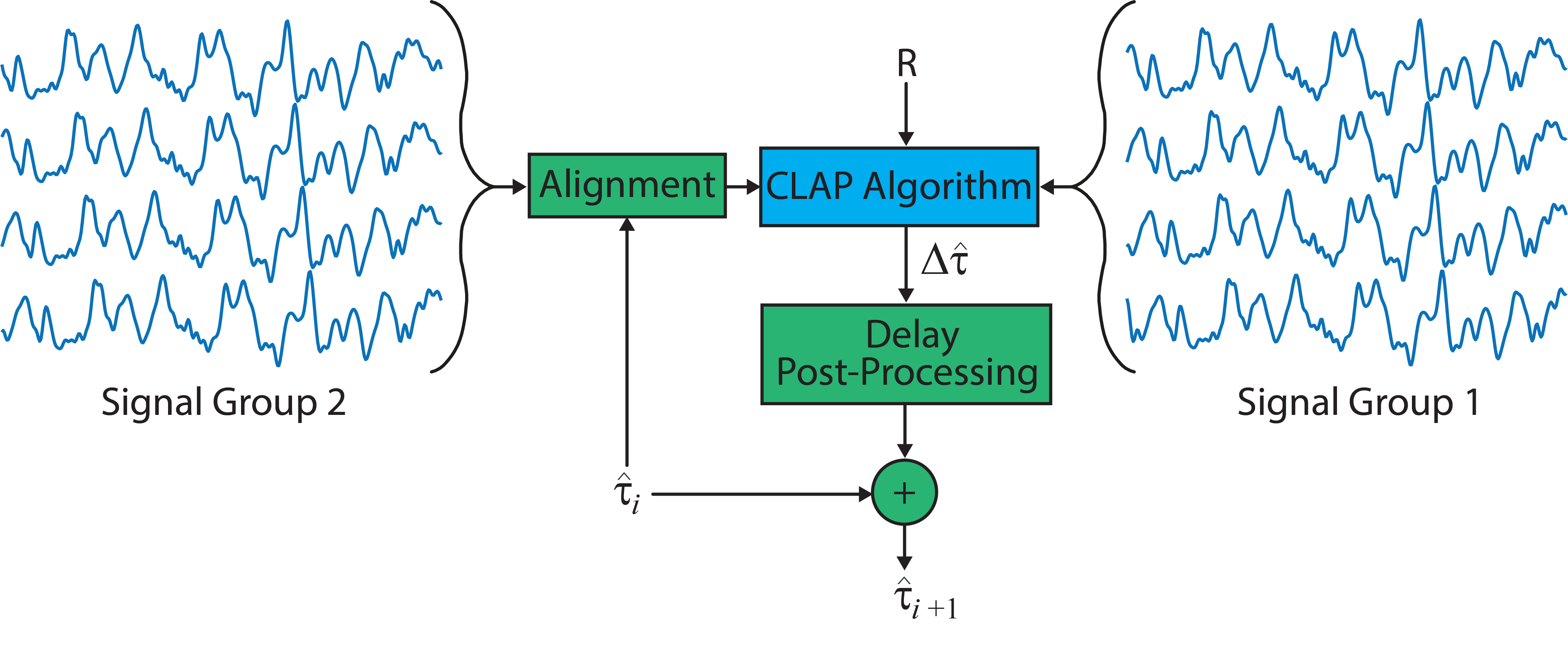
We use our CLAP framework to estimate conduction velocity (CV) from high-density surface electromyography (sEMG) recordings [6], [14]. CV describes the speed of propagation of motor unit action potentials (MUAPs) along the muscle fibre and is an important factor in the study of muscle activity revealing information regarding pathology, fatigue or pain in the muscle.